目前研究表明,除了大小形态外,形态学参数如长宽比AR、尺寸比SR,血流动力学参数如壁面切应力WSS、剪切震荡指数OSI也均在破裂动脉瘤和非破裂动脉瘤中显著差异。但这些参数不便于临床决策参考。流动模式的WSS和OSI很大程度上取决于流入波形,即搏动指数PI,PI与IA破裂状态高度相关。
——摘自文章章节
【REF: Asgharzadeh H, et al.Neurosurgery. 2020;nyaa189. doi:10.1093/neuros/nyaa189】
研究背景
先前研究表明,PI与形态学参数组合可以帮助区分动脉瘤是否破裂。并且近期研究报道,目前已开发出一种简单的无量纲参数,凭借几何形状和流动波形来分类侧壁动脉瘤的流动模式。这个参数称为“动脉瘤数(aneurysm number, ![]() )”,目前发现
)”,目前发现![]() >1主要是环形涡流的形成、运输撞击所致。而
>1主要是环形涡流的形成、运输撞击所致。而![]() <1则形成准静态剪切层。与
<1则形成准静态剪切层。与![]() >1相比,
>1相比,![]() <1的IA具有较低的WSS和OSI,
<1的IA具有较低的WSS和OSI,![]() 可以作为新的参数替代WSS和OSI。本研究旨在研究
可以作为新的参数替代WSS和OSI。本研究旨在研究![]() 是否可用于区分破裂IA及未破裂IA。
是否可用于区分破裂IA及未破裂IA。
研究方法
选取动脉瘤数据库中2007年至2010年共204名患者数据进行回顾性分析,包括破裂IA(n=46)及未破裂IA(n=148),将119名患者数据用于模型构建,其余85名患者数据用于验证模型。
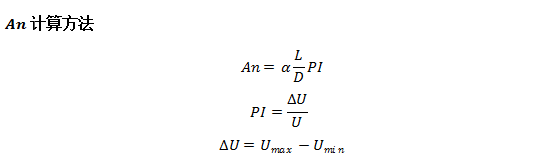
其中D为载瘤动脉直径,U为载瘤动脉内平均流速,![]() 和
和![]() 是一个心动周期内最大和最小流速,L为沿图1中动脉血流方向
是一个心动周期内最大和最小流速,L为沿图1中动脉血流方向![]() 血管扩张区域的长度,在侧壁动脉瘤中为瘤颈W(图1A和1B),在分叉动脉瘤中为
血管扩张区域的长度,在侧壁动脉瘤中为瘤颈W(图1A和1B),在分叉动脉瘤中为![]() (图1C和1D)。对于侧壁及分叉动脉瘤,
(图1C和1D)。对于侧壁及分叉动脉瘤,![]() 分别为1和2。
分别为1和2。
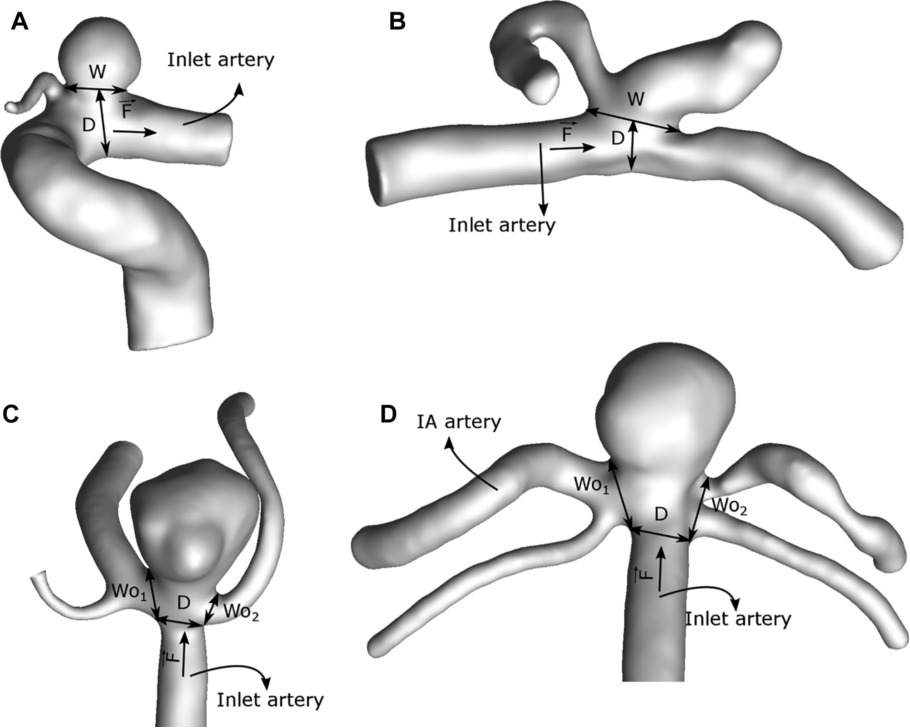
图1. 不同几何形状动脉瘤的![]() 参数计算插图:A和B是侧壁IA示例,C和D是分叉IA的示例
参数计算插图:A和B是侧壁IA示例,C和D是分叉IA的示例
![]() 同时也是动脉瘤中两种竞争现象的时间尺度比率:
同时也是动脉瘤中两种竞争现象的时间尺度比率:
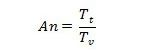
![]()
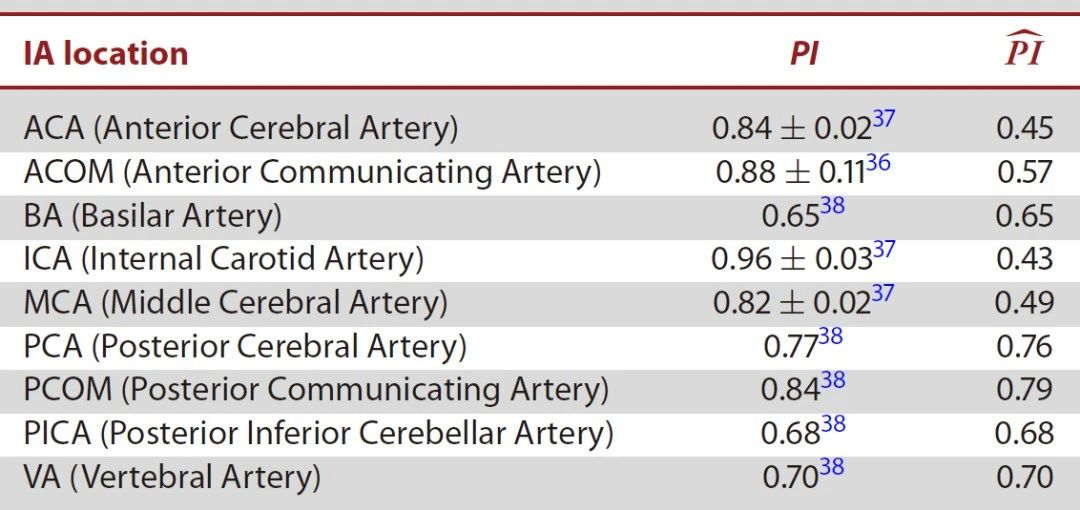
首先,根据文献报道中健康受试者特定部位的平均值估算PI,汇总如表1。其次,由于各个研究报告中PI值不同,且由于受试者健康状况、年龄等混杂因素,本文重新估计每个位置的PI,以便当![]() =1时最大化模型分类能力,
=1时最大化模型分类能力,![]() 是区分破裂和未破裂IA的阈值,该估算PI记为
是区分破裂和未破裂IA的阈值,该估算PI记为![]() ,
,![]() 计算出的记为
计算出的记为![]() ,
,![]() 汇总如表1。
汇总如表1。
表1. 文献中的平均值PI(根据位置划分)及根据训练数据集优化后![]()
研究结果
图2展示了破裂和未破裂IA数据的![]() 分布,表2展示了破裂和未破裂IA的平均
分布,表2展示了破裂和未破裂IA的平均![]() 值,并进行假设检验。破裂
值,并进行假设检验。破裂![]() 和未破裂
和未破裂![]() 组,样本均值
组,样本均值![]() =2.032和
=2.032和![]() = 1.082,样本标准差
= 1.082,样本标准差![]() =1.00和
=1.00和![]() =0.48。总体均数及95%置信区间
=0.48。总体均数及95%置信区间![]() 图3显示了
图3显示了![]() 的分布,IA破裂的样本均值为1.38,IA未破裂的样本平均值为0.63(表2)。假设检验表明,两组
的分布,IA破裂的样本均值为1.38,IA未破裂的样本平均值为0.63(表2)。假设检验表明,两组![]() 的总体均值存在显着差异,当使用阈值
的总体均值存在显着差异,当使用阈值![]() =1来区分破裂IA和未破裂IA时,具有84%敏感性和51%特异度(表2)。类似地,对于
=1来区分破裂IA和未破裂IA时,具有84%敏感性和51%特异度(表2)。类似地,对于![]() (
(![]() 阈值 = 1),敏感性83%,特异度91%。
阈值 = 1),敏感性83%,特异度91%。
表2分别计算了破裂的分叉和侧壁IAs的![]() 和
和![]() 样本均值。针对这两种类型的IA进行t检验,均拒绝H0,表明分叉和侧壁IA破裂数据的和的总体均值大于1。
样本均值。针对这两种类型的IA进行t检验,均拒绝H0,表明分叉和侧壁IA破裂数据的和的总体均值大于1。
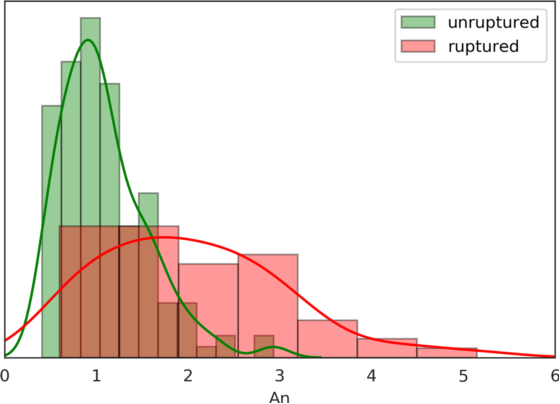
图2. ![]() 数据分布图
数据分布图
表2. ![]() 和
和![]() 总体及分类分析
总体及分类分析
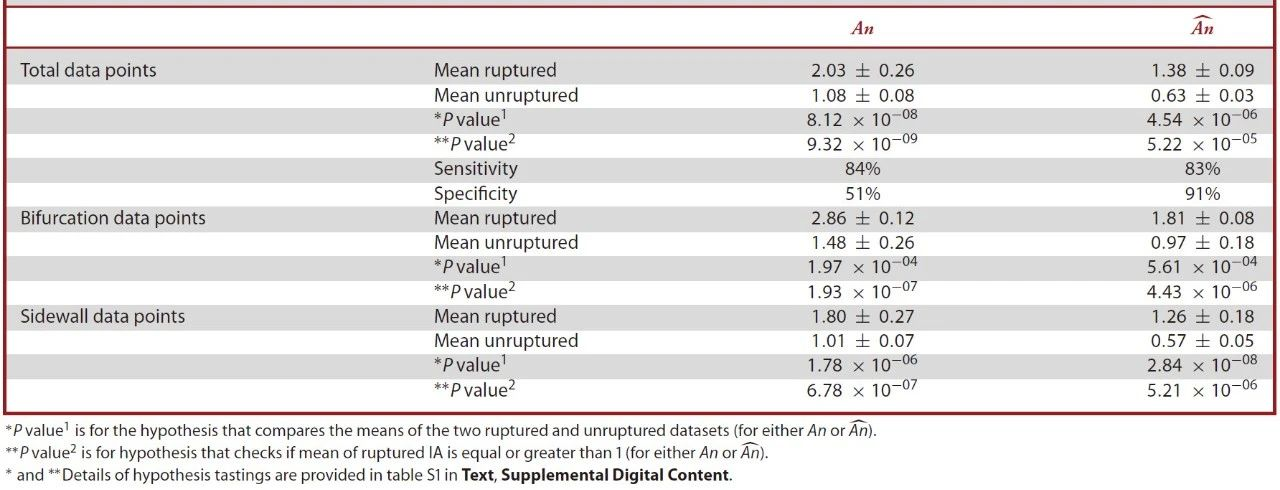
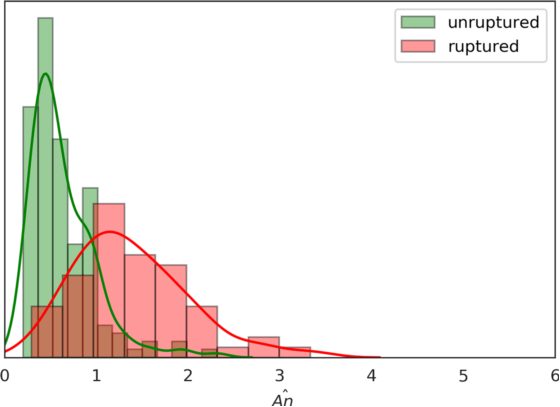
图3. ![]() 数据分布图
数据分布图
表3. ![]() 、
、![]() 、SR及其组合的模型
、SR及其组合的模型
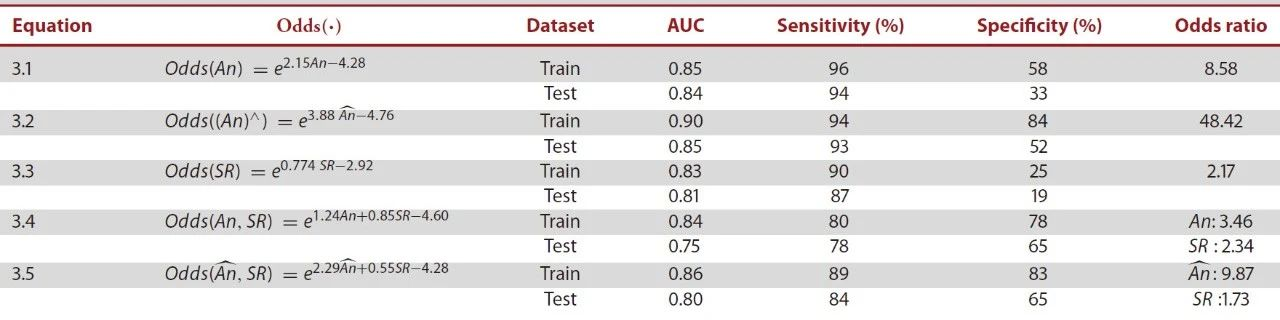
表3中3.1是使用![]() 作为自变量来预测破裂状态。使用测试数据集检验模型预测能力,
作为自变量来预测破裂状态。使用测试数据集检验模型预测能力,![]() 对破裂状态的预测在95%置信水平上具有统计学意义(P=7.38× 10−11)。图4显示了使用3.1预测破裂IA进行训练和测试数据集的ROC图。对于训练数据集,AUC=0.85±0.088,对于测试数据集,敏感性94%,特异度33%。
对破裂状态的预测在95%置信水平上具有统计学意义(P=7.38× 10−11)。图4显示了使用3.1预测破裂IA进行训练和测试数据集的ROC图。对于训练数据集,AUC=0.85±0.088,对于测试数据集,敏感性94%,特异度33%。
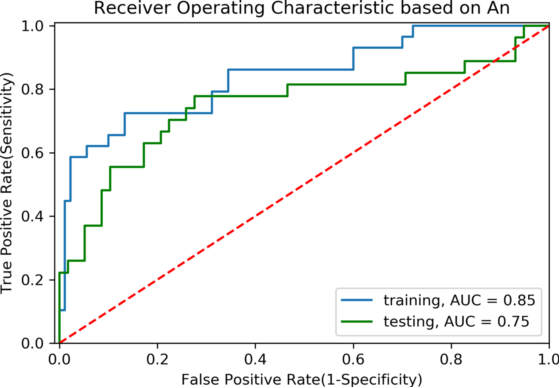
图4. ![]() 模型ROC曲线
模型ROC曲线
3.2使用![]() 作为自变量,
作为自变量,![]() 对破裂状态预测具有统计学意义(P =2.5×10−13)。图5显示了3.2的ROC图。训练数据集AUC=0.90±0.012(敏感性94%,特异度84%)和测试数据集AUC=0.85±0.032(敏感性93%,特异度52%)。这些结果大于
对破裂状态预测具有统计学意义(P =2.5×10−13)。图5显示了3.2的ROC图。训练数据集AUC=0.90±0.012(敏感性94%,特异度84%)和测试数据集AUC=0.85±0.032(敏感性93%,特异度52%)。这些结果大于![]() 模型的AUC。
模型的AUC。![]() 和
和![]() 增加一个单位相关优势比分别为48.42和8.58。通过上述AUC分析得出的最佳阈值分别为1.56和1.04,接近于基于物理分类的阈值1。为了证明基于训练数据库的
增加一个单位相关优势比分别为48.42和8.58。通过上述AUC分析得出的最佳阈值分别为1.56和1.04,接近于基于物理分类的阈值1。为了证明基于训练数据库的![]() 适用于其他数据集,在测试数据集上对其进行了测试。
适用于其他数据集,在测试数据集上对其进行了测试。![]() 、
、![]() 在未破裂和破裂的IA之间发现了统计学上的显著差异(P<0.001)。
在未破裂和破裂的IA之间发现了统计学上的显著差异(P<0.001)。
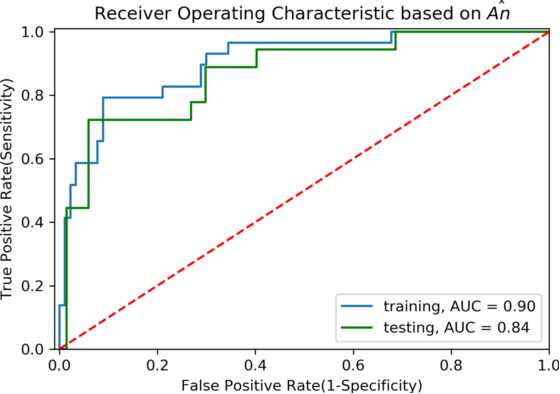
图5. ![]() 模型ROC曲线
模型ROC曲线
与WSS和OSI结合使用的血液动力学模型(敏感性75%,特异度84%,AUC=0.85)相比,模型的性能更好(敏感性94%,特异度84%,AUC=0.90±0.012)。此外,与以SR为自变量的已发表形态模型相比,![]() 模型具有更高的敏感性,该模型是从相同的数据集中得出的(即表3中的3.3,AUC=0.83,训练数据集敏感性90%,特异度25%,测试数据集,敏感性87%,特异度19%)。SR增加1个单位相关的优势比为2.17。
模型具有更高的敏感性,该模型是从相同的数据集中得出的(即表3中的3.3,AUC=0.83,训练数据集敏感性90%,特异度25%,测试数据集,敏感性87%,特异度19%)。SR增加1个单位相关的优势比为2.17。![]() 和
和![]() 模型的AUC(训练数据集的
模型的AUC(训练数据集的![]() =0.85,
=0.85,![]() =0.90)大于模型(
=0.90)大于模型(![]() =0.83)。3.4则为(
=0.83)。3.4则为(![]() ,SR)模型,3.5为(
,SR)模型,3.5为(![]() ,SR)模型作为独立变量预测破裂IA,3.4中
,SR)模型作为独立变量预测破裂IA,3.4中![]() 和SR的每单位增加相关优势比分别为3.46和2.34。3.5中
和SR的每单位增加相关优势比分别为3.46和2.34。3.5中![]() 和SR的每单位增加相关优势比分别为9.87和1.73。
和SR的每单位增加相关优势比分别为9.87和1.73。
研究结论
![]() >1表示破裂状态,
>1表示破裂状态,![]() 和
和![]() 对于区分动脉瘤破裂状态是有价值的简便的临床参数,并可能用于辅助决定未破裂动脉瘤的治疗。
对于区分动脉瘤破裂状态是有价值的简便的临床参数,并可能用于辅助决定未破裂动脉瘤的治疗。
即日起“神经介入资讯”更名为“神介资讯





